Codeforces Round #739 (Div. 3) Problem. C

https://codeforces.com/contest/1560/problem/C
Codeforces Round #739 (Div. 3)

C. Infinity Table

TimeLimit	MemoryLimit	Difficulty	Tags
1 S	256 MB	800	implementation math

Attr	SubNo	SolveTime	Time	Memory	Accept?
1	126343911	+14min (70m)	30 ms	3600KB	Accepted

---

문제 요약

2차원배열 가장 왼쪽 위부터 시작하는 table이 있다. 이table은 다음과같은 패턴으로 순서대로 생성이 된다.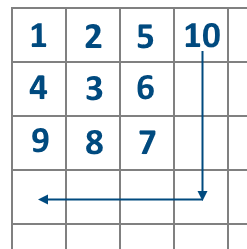

위와같은 패턴으로 table이 무한정 생성될 때 k가 존재하는 행과 열을 구하여라.

피드백

Input

1-st line : Testcase (1 <= t <= 100)
각 Testcase 마다
t-th line : 1개의 정수 (1 <= k <= 10⁹)

Output

각 Testcase 마다
2개의 정수 (r, c >= 1) space로 구분 : k가 위치하고있는 열과 행

---

문제 풀이

또 800점 문제이다. 또한 패턴만 구하면 간단하게 해결할 수 있었다.

0번째 열을 확인해보면 각각 n번째 행의 원소들이 n의 제곱인것을 확인할 수 있다.
다르게 말하면 0번째 행의 0보다 큰 n번째 열의 원소는 n-1의 제곱 + 1이라는 사실도 성립된다.
또한 변화하는 행과 열의 종류가 변경되는 시점은 n-1의 제곱 + (n-1)이기 때문에 k의 위치는 쉽게 구할 수 있었다.

---

최종 해설

먼저 정수형 sq를 선언하여 k의 제곱근(소수점부분은 제외)을 구하였다.

만약 소수점을 제외한 sq의 제곱이 k와 같다면, k의 위치는 0열 sq행으로 고정되기 때문에 예외를 두어 처리를 해 주었다.

다음으로 알아야 하는것은 k가 위치하고 있는 곳이 열이 변경되는 구간인지, 행이 변경되는 구간인지 알 필요가 있다.
먼저 행과 열이 바뀌는 구간은 sq의 제곱 + sq로 구할 수 있다. (행과 열이 만나는 시점)

따라서 해당 값보다 크게 되면, 가로로 배치되는 시점이므로 행의 위치는 sq+1로 고정이며 열의 위치는 sq+1의 제곱에서 k값을 뺀 값이 k가 위치하는 열의 번호가 된다.

또는

행과 열이 만나는 시점보다 k의 값이 작게 되면, 세로로 배치되는 시점이므로 열의 위치는 sq+1로 고정이며 행의 위치는 k에서 sq의 제곱을 뺀 값이 된다.

---

최종 코드

#include <iostream>
#include <math.h>
 
using namespace std;
 
int main(void) {
    int TestCase = 0;
    cin >> TestCase;
    while (TestCase --)
    {
        int k;
        cin >> k;
        int sq = (int)sqrt(k);
        if(sq*sq == k) {
            cout << sq << " " << 1 << endl;
            continue;
        }
        if(k > sq*sq+sq) 
            cout << sq+1 << " " << sq-(k-(sq*sq)-sq)+2 << endl;
        else 
            cout << k-(sq*sq) << " " << sq+1 << endl;
    }
    
    return 0;
}

느낀점

어렵지 않았다. 간단한 공식을 알아내면 쉽게 풀 수 있는 문제였다.
앞에서 뻘짓한게 아까웠다..